CMOSアニーリングの顧客適用に向けた量子コンピュータ技術の応用
ハイライト
近年,交通渋滞や少子高齢化などの複雑な社会課題が顕在化しているが,それらの課題を解決するためには膨大な計算を行う必要があり,その大部分は組合せ最適化問題の計算である。従来のコンピュータでは最適化するパラメータの数が増えるに従い,計算に要する時間や消費エネルギーが飛躍的に増大してしまうことが課題であった。
本稿では,そうした課題を解決するために,昨今注目を集める量子コンピュータに着想を得て,日立が2015年に開発した新型コンピュータCMOSアニーリングについて,概要や開発背景などを紹介する。また,さまざまな業態でニーズがある要員の勤務シフトを決定する「要員配置最適化問題」を例に,この先進技術をいかに顧客業務に適用していくことができるか,その価値と可能性を解説する。
1. はじめに
IoT(Internet of Things)の進展によって大量のデータが取得されるようになり,それに伴い,そのデータ処理を行うために必要となる計算量は増大している。従来は収集されたデータは数値計算に使われることが多かったが,昨今では,スマートな社会の実現をめざしてさまざまなシステムを最適化するための最適化処理など,これまでと異なる用途に使われ始めている。一方で,半導体の微細化は終焉(えん)が近いと言われており,従来のノイマン型※1)計算機の性能向上は頭打ちとなっている。そこで,最適化処理を効率よく実行する計算手法として,アニーリングマシンというコンピュータが提案されている。アニーリングマシンでは,磁性体の振る舞いを表す統計力学上のモデルであるイジングモデルを物理現象として用いて組合せ最適化問題を処理するもので,昨今話題の量子コンピュータの世界でもアニーリング方式を採用する量子コンピュータが存在する。
日立は,量子を使わず半導体回路を用いてイジングモデルを模擬するCMOS(Complementary Metal Oxide Semiconductor)アニーリングマシンを提案した。このCMOSアニーリングマシンのプロトタイプを試作し,実際に組合せ最適化問題が解けることを確認している。
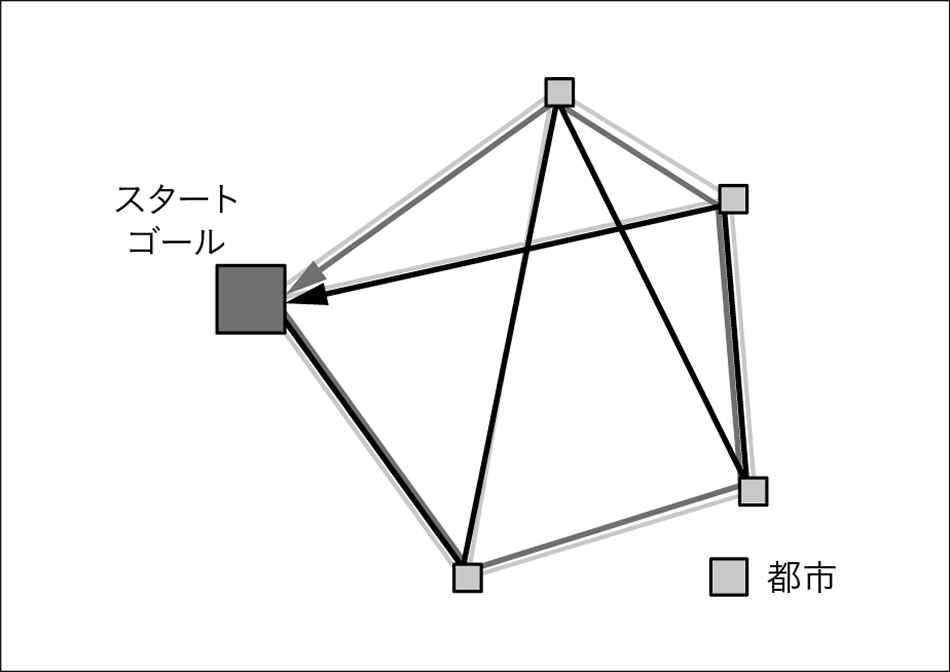
組合せ最適化問題とは,与えられた条件の中で評価指標を最大(または最小)とするパラメータの組合せ(解)を探索する問題である。最も有名な組合せ最適化問題は,図1に示す巡回セールスマン問題が挙げられる。この問題は,都市の数が増えると経路の組合せの数が爆発的に増加し,最短の経路を求めるのが難しくなる。
- ※1)
- 現在広く一般的に使われるコンピュータで,CPUを使い順次命令の実行やデータ処理などを行う計算機。
2. 最適化問題に挑む人類の歴史
生産計画や輸送問題などの最適化問題を効率的に解くため,古来よりさまざまな技術が開発されてきた。特に有名な技法がジョージ・ダンツィーグによって1947年に開発された,線形計画法※2)の解法である単体法である。また,同時代に計算機科学に関する理論および電子技術が蓄積されてコンピュータが登場した。大量の計算を高速に実行するコンピュータならではの活用法の一つが,1950年代前半に登場したモンテカルロ法※3)である。このように最適化技法および計算機の発展が相まって,20世紀後半にノイマン型計算機で最適化アルゴリズムを実行することによって最適化問題が解かれてきた。
2000年代に入ると,現在も最適化問題を解くために広く用いられているアニーリング方式1)をハードウェアで再現した量子アニーリングマシン2)が発表された。以前から研究されてきた汎用的な使い方が期待できるゲート型の量子コンピュータとは異なり,計算用途は組合せ最適化に限定されるものの,実際に動作する量子計算機であったために注目を集めた。計算時間などの面で優れていると期待されているものの,動作環境が絶対零度近くでなければならないことや,量子性を保つために大規模化が困難であるなどの課題も指摘されている。
上述の課題を解決すべく,日立は半導体技術を活用したCMOSアニーリングマシン(SA:Simulated Annealing)を2015年に発表した3)。また,大規模並列計算による解探索高速化を実現したモメンタム・アニーリング(MA:Momentum Annealing)と呼ぶアルゴリズムを2019年に発表した4)。
以降,CMOSアニーリングマシン(SA),モメンタム・アニーリング(MA)を合わせてCMOSアニーリングと表記する(図2参照)。
図2|ソルバの歴史 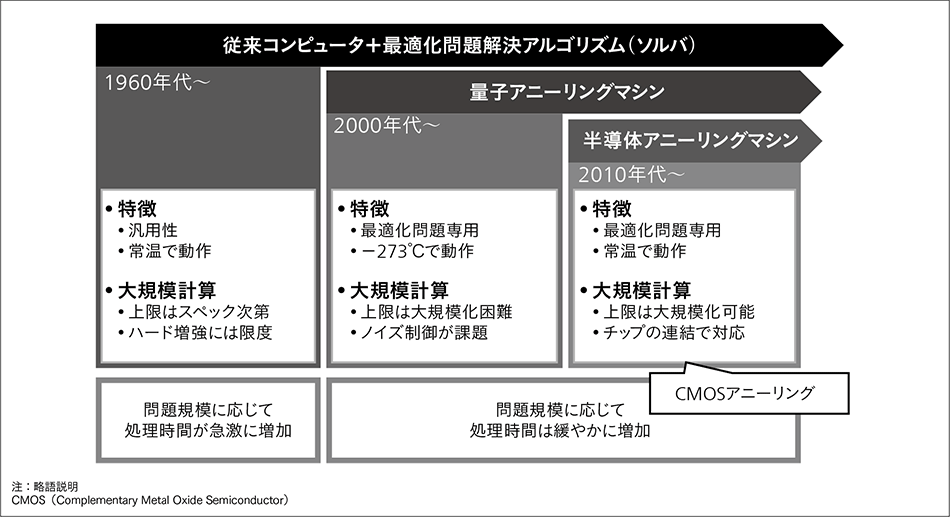 最適化問題を解く手法の変遷と,それらの特徴について示す。従来コンピュータ+最適化問題解決アルゴリズムは大規模計算に課題がある。また量子アニーリングマシンは-273℃に冷却する必要があり,多大なコストが必要となる。
最適化問題を解く手法の変遷と,それらの特徴について示す。従来コンピュータ+最適化問題解決アルゴリズムは大規模計算に課題がある。また量子アニーリングマシンは-273℃に冷却する必要があり,多大なコストが必要となる。
- ※2)
- 守るべきルール,最小化,最大化したい目的がともに一次式で定義される場合に,最良の解を求める数学的手法。
- ※3)
- 乱数を発生させて試行を繰り返し,さまざまなシミュレーションを実施する数値計算手法。
2.1 顧客の期待とマーケット
今後の社会課題において,最適化計算は重要な地位を占めると予測される。例えば金融分野ではリスク低減に向けたポートフォリオ最適化,都市インフラ分野では省エネルギー社会の実現に向けた渋滞削減などが考えられる。これらの最適化は今後ますます重要となり,2025年には市場が1兆円になると試算されている5)。
2.2 日立の位置づけ
最適解を求める手法の一つであるアニーリング法※4)を活用した最適化ソリューションは,CMOSアニーリングをはじめとして,いくつかの企業から発表されている。各方式の特長を表1に示す。
ここで重要な比較軸が二つあり,それはスピン数と結合型である。ここで言うスピンとは最適化したい対象に相当するもので,スピン数とはまさにその数のことである。この数が大きければ大きいほど,沢山の対象を扱った最適化問題を解くことが可能となる。なお,スピン数は問題の規模と表現されることもある。
また結合型はスピンとスピンのつながり方を意味するもので,スピンどうしがつながっている場合はその二つのスピンは互いに影響を及ぼしうる。全結合はすべてのスピンが自分以外の他のスピンとつながっていることを意味し,疎結合は,特定のスピンとしかつながっていないことを意味する。
CMOSアニーリングのスピン数は他社と比べても最大のスピンを有している。なお,最適化の対象が数百~数千程度の小規模問題ならば従来手法でも解くことができる。アニーリング技術に求められているのは大規模問題に対する高速な解探索であり,CMOSアニーリングはこの要求を満たす。
CMOSアニーリングには,全結合の問題に対応したMAと,疎結合の問題に特化したCMOSアニーリングマシン(SA)の二つの方式がある。解きたい問題の結合型に合わせ,より適切な方式を選択することができるため,多岐にわたる最適化問題に対応可能である。いずれの観点においてもCMOSアニーリングはトップの水準を実現している(同表参照)。
表1|アニーリング技術のベンチマーク 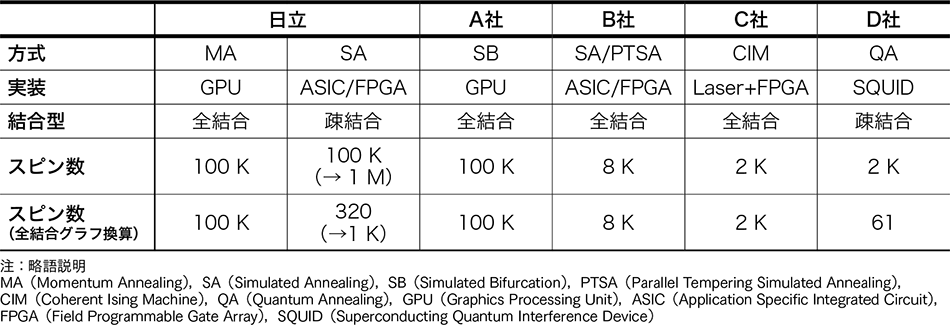 日立は,MA,SAという2方式のアニーリングマシンが提供可能で,解きたい問題に合わせて選択が可能である。また,解ける問題の規模に相当するスピン数も世界最大である。
日立は,MA,SAという2方式のアニーリングマシンが提供可能で,解きたい問題に合わせて選択が可能である。また,解ける問題の規模に相当するスピン数も世界最大である。
- ※4)
- 金属の焼きなましを応用し,温度に相当するパラメータ値を徐々に下げることで,最適な解を見つけようとする手法。
3. CMOSアニーリングを適用していく際の課題
前述のように,CMOSアニーリングはこれまでにない大規模な組合せ最適化計算を高速に実行可能であるが,これをビジネスに適用していくためには二つの課題を克服する必要がある。
一つ目は,顧客業務をアニーリング方式で解けるモデルに落とし込むこと,あるいはアニーリング方式を適用可能な業務を見つけ出すことである。顧客は組合せ最適化の専門家ではないため,どの業務がアニーリングに適しているか,どうやったらCMOSアニーリングで解けるよう定式化できるかを判断することは難しい。特にアニーリング方式では現実世界をスピン,磁場,相互作用で表すための専門知識が必要であり,これを顧客が実施するのは困難である。
一方で技術者は典型的な問題を解く方法は知っているものの,現実のビジネス課題をモデルに取り込むのは容易ではない。それを実現するには顧客の課題を読み取って組合せ最適化問題に落とし込み,さらにそれをCMOSアニーリングで解ける形に落とし込むことが必要であり,顧客業務に対する深い理解と,それをモデル化する想像力が必要である。
そこで日立は,(1)実際に顧客からビジネス課題をヒアリングし,(2)CMOSアニーリングで解くための定式化を実行し,(3)実際のデータを使って最適化を実施し,(4)その結果に対して顧客からフィードバックをもらう,というサイクルを繰り返すことで顧客業務とCMOSアニーリングに対する理解を深め,顧客課題を解決するモデルを創り上げた。
二つ目の課題は,従来手法と比べたCMOSアニーリングの優位性をいかに訴求するかである。例えばポートフォリオ最適化では,従来手法で1秒で解いていたものを0.01秒で解けるようになったとしても,CMOSアニーリングを使うユーザーは,得られた結果に対し判断を下すため,そこまで大きなメリットは生み出せず,新技術を導入する意欲が生まれない。そこで,顧客を巻き込みながら,CMOSアニーリングの大規模で高速な計算力が強みを発揮し,かつ顧客業務も大きく改善するようなモデルを考案した。
これらの取り組みはまだ始まったばかりで,今後も継続的に実施していくべきものである。次章では,そのような取り組みの一例として,CMOSアニーリングを金融機関のコールセンター業務の最適化に適用した場合について解説する。
4. 要員配置最適化の事例
ここでは,現在CMOSアニーリング適用検証中の事例のうち,コールセンターにおける要員配置最適化の試みについて紹介する。昨今のデジタルトランスフォーメーションの流れの中で,コールセンターに代表されるカスタマーサポートの重要性は,業種を問わず増してきている。特に,年々労働人口が減少している日本においては,少ない要員でも質の高いカスタマーサポートを提供し続けることが喫緊の課題となっているため,顧客からの関心も高い。
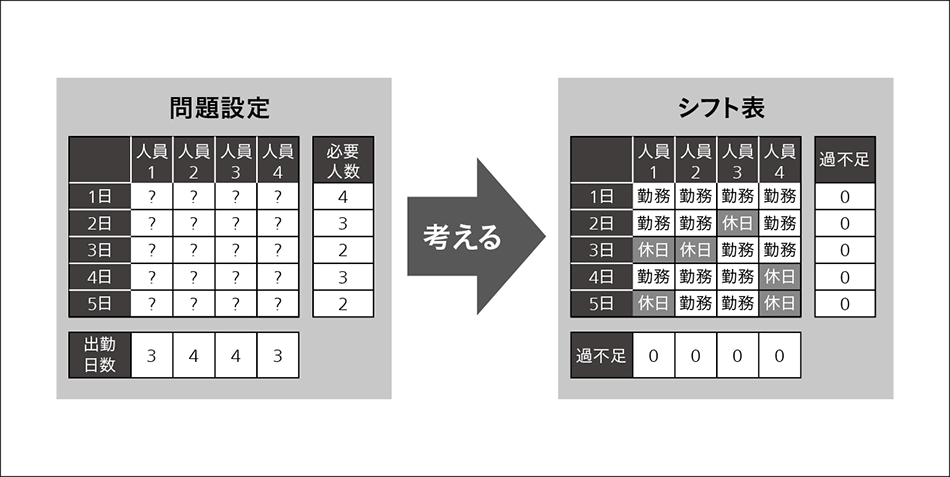
4.1 最適化問題としてのシフト作成業務
コールセンターにおける要員配置最適化の具体的な例として,電話を受ける要員のシフト表(勤務表)の作成業務を取り上げる。シフト作成業務を組合せ最適化問題として表現すると,「日ごとの必要人数を満たし,かつ,各要員に定められた出勤日数も満たすように,どの日にどの人員を勤務させるかを選択する作業」になる(図3参照)。この例では問題を非常に単純化しているが,それでも4人×5日分の20マスに対して「勤務」か「休日」かを選ぶ組合せの数は2の20乗で約100万通りになる。実際に顧客が作成しているシフト表は数百人分にも及ぶことがあり,この時の組合せの数は天文学的な数字になる。そのため,シフト作成専門の担当者が,毎月,長い時間をかけてシフト表を作成しているという現状がある。
4.2 コールセンターの要員配置最適化における課題
コールセンターのシフト作成業務において最も重要な観点の一つは,予測された電話量に対し,どれだけ正確に適切な人数を割り当てることができるかである。電話量に対して人員の数が不足すれば,待ち時間の増加に伴う顧客満足度の低下や,業務負荷増大によるオペレータ満足度の低下を招く。一方で,人員を過剰に割り当ててしまった場合は人的コストの増加原因となる。日々変化する需要の波に合わせ,いかに過不足なく人員を供給できるかがコールセンターの質を左右する。
さらに言えば,単に必要人数がそろうだけでは不十分だというケースが多い。人員によって知識量や熟練度に差があるため,かかってくる電話の内容に応じて,必要なスキルを持つ人員を適切に割り当てる必要がある。
しかし,市販されているシフト作成支援ツールには,そこまでの機能を搭載しているものは少ない。30分単位で需要の波に合わせたタイムテーブルを作成することまではできても,それを各人員が持つスキルや熟練度を考慮したうえで実施することは,計算規模や制約条件の複雑さの観点から非常に難しい。言い換えれば,大規模な組合せ最適化問題を高速に解くことができる技術がなければ,細かな粒度で多数の制約条件を考慮したシフト作成をすることは困難である。
複数のスキルを考慮したタイムテーブルを作成する場合の組合せの数として,例えば100名,4種類のスキル,20日,8コマ/日を選択する問題の場合であれば,4(100*20*8)=9.12*109632となり,まさに天文学的な数字となる。
4.3 CMOSアニーリングの適用
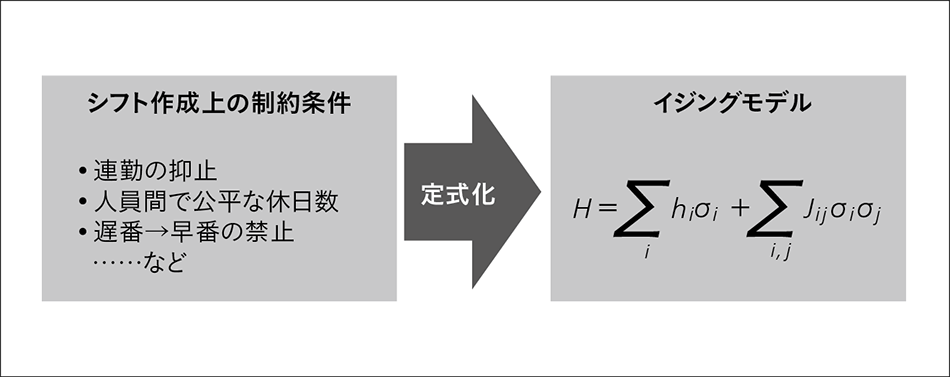
CMOSアニーリングを用いてシフト作成をするためには,顧客が考慮している制約条件をすべて定式化する必要がある。実際にシフト作成者が考慮している観点は,明文化されているものから暗に設定されているものまで多岐にわたる。一例を挙げると,連勤の抑止,人員間で公平な休日数,禁止パターンの設定(例:遅番→早番の禁止),ベテランと新人のバランス,個々人が持つ対応可能スキルなどがある。このような制約条件を正確に定式化するには,複数の制約を矛盾なく数式に変換する数学力と,顧客から正確な要件を聞き出すコンサルティング能力が必須となる(図4参照)。
4.4 CMOSアニーリングの優位点
CMOSアニーリングの優位点としてまず挙げられるのが,計算スピードである。一般的なシフト作成支援ツールは,CPU(Central Processing Unit)上で専用のアルゴリズムなどを用いて最適化問題を解いている。そのため,問題の規模や制約が増加するにしたがって計算時間が急増する傾向にある。一方でCMOSアニーリングは問題規模が大きくなっても計算時間の増え方が比較的緩やかであるという特徴があるため,大規模な問題でも高速に解くことができる。そのため,月次で実施するシフト作成時間そのものが短縮されるのはもちろんのこと,急な需要増やオペレータの急な欠勤に合わせ,日次や数時間おきにタイムスケジュールを修正するという,従来にない運用が可能になる。
さらに,対応可能な問題規模が大きいという点もCMOSアニーリングの強みである。大規模な問題が解けるということは,より細かな粒度で精緻にシフトを作成することができることを意味する。例えば,人員ごとのスキルや熟練度を考慮しながら,需要の波に合わせて休憩時間や業務内容を最適に割り当てるタイムスケジュールを作ることができる。現在,このような粒度の細かいシフトをCMOSアニーリングを用いて作成し,実業務に適用する検証を複数の顧客と進めているところである。これにより,従来のシフト作成手法では考えられなかったような運用の仕方が見つかることを期待している。
5. おわりに
本稿では,事例を踏まえCMOSアニーリングをユーザーへ適用していく際の課題について考察した。
優れた技術があったとしても,その使い道や,使い方を正しく導かないと果実を得られない。果実を得るには,以下の要件が必要である。
- まず知ってもらう
一人でも多くの人が「その問題は最適化問題かも」と気付いてもらえるような,分かりやすい事例を示し,ディスカッションの場を共有する。 - 展開できる人財の育成
当該技術に精通し,定式化ができる人財が必要不可欠である。こういった人財はすぐには育たないことから,PoC(Proof of Concept)や提案の場を経験させ育成するとともに,場合によっては一人の人財にすべてを求めるのではなく,分業させるといった組織マネジメントも必要である。
この課題は,CMOSアニーリングに限らず先端技術全般の課題であるため,今回のプロジェクトで成果や課題を洗い出し,顧客との協創を展開する多くのプロジェクトへそのノウハウを提供していきたいと考える。
参考文献など
- 1)
- T. Kadowaki et al.: Quantum Annealing in the Transverse Ising model, Physical Review E, Vol. 58, Iss. 5, 5355(1998.11)
- 2)
- M. W. Johnson et al.: Quantum annealing with manufactured spins, Nature, Vol. 473, Iss.7346, pp. 194-198(2011.5)
- 3)
- M. Yamaoka et al.: A 20k-spin Ising Chip to Solve Combinatorial Optimization Problems With CMOS Annealing, IEEE Journal of Solid-State Circuits, Vol. 51, Iss. 1, pp. 303-309(2015.12)
- 4)
- T. Okuyama et al.: Binary optimization by momentum annealing, Physical Review E, Vol. 100, Iss. 1, 012111(2019.7)
- 5)
- 量子コンピュータの開発動向と市場予測に関する調査